| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- ethers v6
- redux toolkit 설명
- 스마트 컨트렉트 함수이름 중복
- vue기초
- erc4337 contract
- Vue
- SBT표준
- ethers websocket
- cloud hsm 사용하기
- cloud hsm 서명
- 러스트기초
- rust 기초
- 오블완
- ethers typescript
- git rebase
- 티스토리챌린지
- 러스트 기초 학습
- 스마트컨트렉트 함수이름 중복 호출
- ethers type
- 계정추상화
- ambiguous function description
- 체인의정석
- erc4337
- redux 기초
- 머신러닝기초
- 러스트 기초
- 스마트컨트렉트 예약어 함수이름 중복
- Vue.js
- cloud hsm
- 컨트렉트 동일한 함수이름 호출
- Today
- Total
체인의정석
컴파운드 분석 2 편) 컴파운드에서의 이자율 계산 본문
0. 이자 모델 계산하기
출저 : https://ianm.com/posts/2020-12-20-understanding-compound-protocols-interest-rates
Understanding Compound protocol's interest rates
A deep dive into the factors that calculate Compound's interest rates.
ianm.com
https://a2-finance.com/ko/calculators/%EB%AA%A8%EB%93%A0-%EA%B3%84%EC%82%B0%EA%B8%B0/%EB%B3%B5%EB%A6%AC-%EA%B3%84%EC%82%B0%EA%B8%B0
복리 계산기(공식과 예시 포함)
복리를 통해 얼마나 벌 수 있는지, 복리와 단리는 어떻게 다른지 무료로 배울 기회. 이 글에서 예시를 통해 복리를 계산하는 공식을 알 수 있습니다.
a2-finance.com
기본적인 복리 계산기는 다음과 같다.
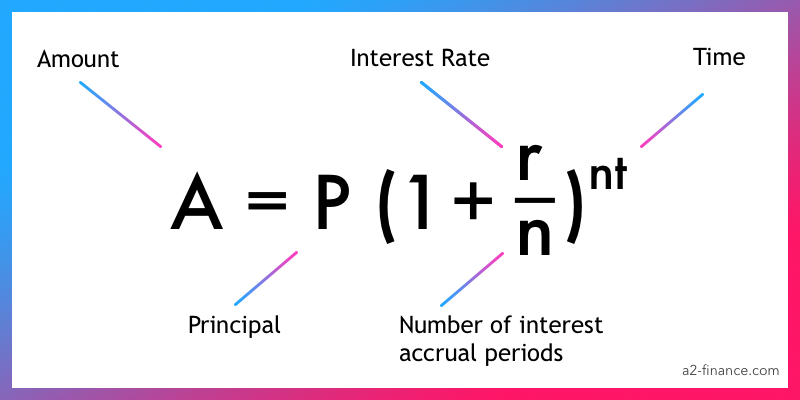
복리 공식은 무엇입니까?
보통 복리 공식은 P x (1 + r/n)nt 입니다. P는 최초 투자 금액, r은 이자율, n은 이자 발생 기간, t는 연 단위 전체 투자 기간입니다.
컴파운드에서 복리의 단위는 블록의 개수이다.
따라서 Number of interest accrual periods 를 1/n으로 두는게 일반적이라고 하면 일단위 로 계산하여 하루에 존재하는 블록의 개수를 1/n 자리에 넣어주어야 한다.
일일 대출/예금 이자율의 경우 기본 이율 r 에다가 하루에 발생한 블록의 개수를 곱해주고 거기에 기본 이율이 10**18 기준으로 계산되어있으므로 이를 나누어주면 된다.
그렇다면 P의 경우 원금이 될 것이고 원금에 (기본 이율 * 하루 발생한 블록의 수 + 1) 이 부분은 (1+ r/n)이 되는 것이고 지수승 nt의 경우 연간 기준 단위가 얼마나 되는지 를 나타내는 수치이기 때문에 1년은 365일 즉 365 승을 제곱해주면된다.
P를 제외하고 본다면 나머지
((기본 이율 * 하루 발생한 블록의 수 + 1) ** 365 -1 ) * 100 이 기본적인 APY 산출 공식이 되게 된다.
이는 아래 페이지에서도 산출이 가능하다.
https://docs.compound.finance/v2/#protocol-math
Rate = cToken.supplyRatePerBlock(); // Integer
Rate = 37893566
ETH Mantissa = 1 * 10 ^ 18 (ETH has 18 decimal places)
Blocks Per Day = 7200 (12 seconds per block)
Days Per Year = 365
APY = ((((Rate / ETH Mantissa * Blocks Per Day + 1) ^ Days Per Year)) - 1) * 100
그럼 여기서 컨트렉트 내부적으로 살펴봐야할 변수는 바로 Rate이다.
아래 컨트렉트에 대한 분석을 통하여 Rate를 구해보도록 하겠다.
1. CToken의 Constructor
Comptroller 주소,
Interset Rate Model 주소
initalExchange rate mentisa = 최초 교환 비율
=> 먼저 interset rate model을 살펴보기로 하였다.
2. JumpRateModel 사용
특정 이용률을 넘어갔을 때 추가적인 이자 수익이 발생하는 모델
2-1. Constructor
/**
* @notice Construct an interest rate model
* @param baseRatePerYear The approximate target base APR, as a mantissa (scaled by 1e18)
* @param multiplierPerYear The rate of increase in interest rate wrt utilization (scaled by 1e18)
* @param jumpMultiplierPerYear The multiplierPerBlock after hitting a specified utilization point
* @param kink_ The utilization point at which the jump multiplier is applied
*/
constructor(uint baseRatePerYear, uint multiplierPerYear, uint jumpMultiplierPerYear, uint kink_) public {
baseRatePerBlock = baseRatePerYear.div(blocksPerYear);
multiplierPerBlock = multiplierPerYear.div(blocksPerYear);
jumpMultiplierPerBlock = jumpMultiplierPerYear.div(blocksPerYear);
kink = kink_;
emit NewInterestParams(baseRatePerBlock, multiplierPerBlock, jumpMultiplierPerBlock, kink);
}baseRatePerYear = 기본 이자율 비율
multiplerPerYear = 이자율에 대한 증가 비율
jumpMultiplierPerYear = 특정 이용률 이상이 되면 증가하는 이자율에 대한 비율
kint = 특정 점프 멀티플라이어가 작동하는 이용률 시점
2-2. utilizationRate
For example: given that reserves are 0, if Alice supplies $500 USDC and Bob supplies $500 USDC, but Charles borrows $100 USDC, the total borrows is $100 and the total cash is 500 + 500 - 100 = 900
, so the utilization rate is 100 / (900 + 100) = 10\%.
Alice : 500 달러 공급
Bob: 500 달러 공급
Charles : 100 달러 대출
이용률 = 100/ ((500+500 -100) +100) => 10%
그리고,
- refers to the amount of a borrowed.
- Cash_a refers to the amount of a left in the system.
- Reserves_a refers to the amount of a that Compound keeps as profit.
/**
* @notice Calculates the utilization rate of the market: `borrows / (cash + borrows - reserves)`
* @param cash The amount of cash in the market
* @param borrows The amount of borrows in the market
* @param reserves The amount of reserves in the market (currently unused)
* @return The utilization rate as a mantissa between [0, 1e18]
*/
function utilizationRate(uint cash, uint borrows, uint reserves) public pure returns (uint) {
// Utilization rate is 0 when there are no borrows
if (borrows == 0) {
return 0;
}
return borrows.mul(1e18).div(cash.add(borrows).sub(reserves));
}이용률 : 캐시, 대출, 컴파운드의 이자(비축량) - 현재 사용되지 않음
U = Borrows/(Cash+Borrows)
만약, 대출한 자산이 0이라면 이용률도 0
그 외에는 (Borrows * decimal) / (cash in market + borrows - reserves)
즉, 총 빌린돈에서 총 마켓 유통량 + 빌린돈 - 컴파운드의 이자수익 을 나눈 값이다.
최신버전의 이용률
/**
* @notice Calculates the utilization rate of the market: `borrows / (cash + borrows - reserves)`
* @param cash The amount of cash in the market
* @param borrows The amount of borrows in the market
* @param reserves The amount of reserves in the market (currently unused)
* @return The utilization rate as a mantissa between [0, BASE]
*/
function utilizationRate(uint cash, uint borrows, uint reserves) public pure returns (uint) {
// Utilization rate is 0 when there are no borrows
if (borrows == 0) {
return 0;
}
return borrows * BASE / (cash + borrows - reserves);
}
2-3. Borrow/Supply Rate
이론 - 기본적인 이자율 계산 모델
Supply Interest Ratea=Borrowing Interest Ratea∗Ua∗(1−Reserve Factora)
- is the utilization rate of a
- is the percentage of the spread between the supply and borrow rates that the protocol keeps as profit
- is the interest rate that borrowers should pay for a
총 공급 이자 율 = 빌린 이자율 * 사용률 * (1 - 컴파운드 이용 수수료)
컴파운드의 표준적인 이자 비율 모델
예시)
- 총 공급량 : 10000 개, 이용률 10%인 상황
- base rate 2 % + multiplier 30% 인 상황
util * multiplierPerBlock / BASE) + baseRatePerBlockBorrow Intererst rate = 30% * 10% + 2% = 5%
대출 이자율 = 5%
- reserve factor = 20% 인 상황 (컴파운드가 가져가는 이자수익)
oneMinusReserveFactor = 컴파운드 수수료에 대한 부분
borrow Rate = 대출 이자율 구하는 함수 실행하여 나온 값
rateToPool = 대출 이자율 * 컴파운드 수수료 차감
이용률 * 대출 이자율 * 컴파운드 수수료 차감 = 공급 이자율
이용률이 높아지거나 대출 이자율이 높아지거나 컴파운드 수수료가 낮아지면 공급 이자율이 올라가게 된다.
uint oneMinusReserveFactor = BASE - reserveFactorMantissa;
uint borrowRate = getBorrowRate(cash, borrows, reserves);
uint rateToPool = borrowRate * oneMinusReserveFactor / BASE;
return utilizationRate(cash, borrows, reserves) * rateToPool / BASE;- Supply Interest rate = 5% * 10% * (1-20%) = 0.4%
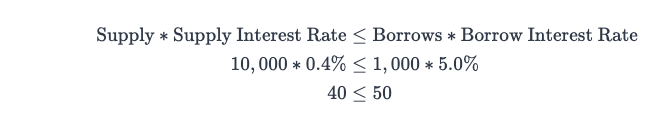
위 공식을 통해서 프로토콜이 돈을 잃지 않음을 체크할 수 있다.
https://compound.finance/markets/WBTC

해당 사이트에 가면 실제 이용률에 따른 이자율의 변화를 직접 볼 수 있다.
예시) 큰 출금이 있는 상황
만약 고래가 8000 만큼의 토큰을 인출한다고 가정해보자.
새로운 이용률은 (8000+1000) / 10000 = 90% 이다.
Borrow시 이자율 : 30% * 90% + 2% = 29%
Supply시 이자율 : 29% * 90% (1-20%) = 20.88%
이렇게 되면 고급 이자율이 무려 5120%가 올라가게 된다.
하지만 대출 이자율은 480%만 올라가게 된다.
이론 - Jump Rate Model
Kink는 이용률의 임계치.
특정 수치를 넘어가면 이율이 점프하게 된다.

- Base rate: 0%/yr
- Multiplier: 5%/yr
- Kink: 80%
- Jump multiplier: 109%
이런식으로 정해져 있다고 하면

다음과 같이 나오게 된다.
uint normalRate = (kink * multiplierPerBlock / BASE) + baseRatePerBlock;
uint excessUtil = util - kink;
return (excessUtil * jumpMultiplierPerBlock/ BASE) + normalRate;
코드
/**
* @notice Calculates the current borrow rate per block, with the error code expected by the market
* @param cash The amount of cash in the market
* @param borrows The amount of borrows in the market
* @param reserves The amount of reserves in the market
* @return The borrow rate percentage per block as a mantissa (scaled by 1e18)
*/
function getBorrowRate(uint cash, uint borrows, uint reserves) public view returns (uint) {
uint util = utilizationRate(cash, borrows, reserves);
if (util <= kink) {
return util.mul(multiplierPerBlock).div(1e18).add(baseRatePerBlock);
} else {
uint normalRate = kink.mul(multiplierPerBlock).div(1e18).add(baseRatePerBlock);
uint excessUtil = util.sub(kink);
return excessUtil.mul(jumpMultiplierPerBlock).div(1e18).add(normalRate);
}
}util을 기준점으로 두어서 이용률을 분기점으로 삼음
kink는 이용률을 기준으로 이자율에 변화가 이루어지는 시점
kink 보다 낮은 경우에는
normalRate + exchessUtil (초과된 이용량) 만큼을 JumpMultiplier 만큼을 곱한 값을 이자율로 더함
최신 버전의 코드
/**
* @notice Calculates the current borrow rate per block, with the error code expected by the market
* @param cash The amount of cash in the market
* @param borrows The amount of borrows in the market
* @param reserves The amount of reserves in the market
* @return The borrow rate percentage per block as a mantissa (scaled by BASE)
*/
function getBorrowRate(uint cash, uint borrows, uint reserves) override public view returns (uint) {
uint util = utilizationRate(cash, borrows, reserves);
if (util <= kink) {
return (util * multiplierPerBlock / BASE) + baseRatePerBlock;
} else {
uint normalRate = (kink * multiplierPerBlock / BASE) + baseRatePerBlock;
uint excessUtil = util - kink;
return (excessUtil * jumpMultiplierPerBlock/ BASE) + normalRate;
}
}
/**
* @notice Calculates the current supply rate per block
* @param cash The amount of cash in the market
* @param borrows The amount of borrows in the market
* @param reserves The amount of reserves in the market
* @param reserveFactorMantissa The current reserve factor for the market
* @return The supply rate percentage per block as a mantissa (scaled by BASE)
*/
function getSupplyRate(uint cash, uint borrows, uint reserves, uint reserveFactorMantissa) override public view returns (uint) {
uint oneMinusReserveFactor = BASE - reserveFactorMantissa;
uint borrowRate = getBorrowRate(cash, borrows, reserves);
uint rateToPool = borrowRate * oneMinusReserveFactor / BASE;
return utilizationRate(cash, borrows, reserves) * rateToPool / BASE;
}supply Rate의 경우
borrowRate를 가져와서 1-Reserve 이자 기본값
rateToPool = borrowRate * (1-reserve)
'블록체인 > 디파이' 카테고리의 다른 글
| compound 청산로직 추가 자료 (0) | 2022.12.27 |
|---|---|
| 컴파운드 분석 3편 - CToken & Comptroller (transfer, 유동성체크, 이자율 체크, 청산) (0) | 2022.12.16 |
| 컴파운드 분석 1 편) 전체 구조와 C Token (1) | 2022.12.07 |
| ZapperIn 분석 (2) | 2022.10.27 |
| UniswapV2 정리4 : fee-on-transfer tokens 함수들 (0) | 2022.10.27 |
