| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 머신러닝기초
- 러스트 기초
- ethers websocket
- erc4337
- 러스트기초
- erc4337 contract
- 스마트컨트렉트 함수이름 중복 호출
- cloud hsm 사용하기
- ethers v6
- redux 기초
- Vue
- cloud hsm
- ethers typescript
- Vue.js
- cloud hsm 서명
- rust 기초
- 러스트 기초 학습
- 컨트렉트 동일한 함수이름 호출
- vue기초
- 오블완
- 스마트컨트렉트 예약어 함수이름 중복
- git rebase
- ethers type
- 체인의정석
- SBT표준
- 계정추상화
- ambiguous function description
- 티스토리챌린지
- 스마트 컨트렉트 함수이름 중복
- redux toolkit 설명
- Today
- Total
체인의정석
머신러닝 스터디 02-선형모델(회귀 편)선형회귀,릿지회귀,라쏘회귀 본문
회귀 중 특성이 하나인 회귀는 선형 모델을 일차 함수를 생각하면 됩니다.
y=ax+b 에서 y는 예측값이 되게 됩니다.
이떄 a와 b는 모델이 학습할 파라미터 입니다. 한마디로 a와 b의 값을 적절히 조절해 가며 정답에 가까운 파라미터를 고르는것이 머신러닝이라 할 수 있겠습니다.
여기서 a는 기울기 입니다. 특성이 많아지게 되면 각각 입력 특성 x에 따라서 가중치 a를 곱한만큼에 b라는 값을 더한만큼이 예측값으로 나오게 됩니다.
mglearn.plots.plot_linear_regression_wave()
회귀를 위한 선형 모델에서 특성이 하나일땐 직선, 2개일때는 평면, 3개 이상일때는 초평면이 되게 됩니다. K이웃근접법과 비교해 보았을때 선으로 분류하는것은 매우 단순해 보이지만 특성을 많이 넣게 되면 더 높은 차원에서 분류가 이루어지게 되어서 성능이 좋다고 합니다.
선형회귀(최소 제곱법)
선형회귀 또는 최소제곱법은 가장 간단하고 오래된 회귀용 선형 알고리즘 입니다. 선형 회귀는 예측과 훈련 세트에 있는 타깃 y 사이의 평균제곱오차를 최소화하는 파라미터 w와 b를 찾습니다. 평균 제곱오차는 예측과 타깃값의 차이를 제곱하여 더한 후에 샘플의 개수로 나눈 것입니다.
일단 책에 있는 코드와 다르게 모듈이 없어져서 생긴 에러가 있어서 아래 링크를 통해 다음 2번째 import문 코드를 추가하였습니다.
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=42)
lr=LinearRegression().fit(X_train,y_train)
https://stackoverflow.com/questions/30667525/importerror-no-module-named-sklearn-cross-validation
ImportError: No module named sklearn.cross_validation
I am using python 2.7 in Ubuntu 14.04. I installed scikit-learn, numpy and matplotlib with these commands: sudo apt-get install build-essential python-dev python-numpy \ python-numpy-dev python-s...
stackoverflow.com
파라미터 w는 가중치 또는 계수라고 하며 lr객체의 coef_속성에 저장되어 있고 편향 또는 절편 파라미터 b는 편향 또는 절편 파라미터는 intercept_ 속성에 저장되어 있습니다.
print("lr.coef_:{}".format(lr.coef_))
print("lr.intercept_: {}".format(lr.intercept_))lr.coef_:[0.39390555] lr.intercept_: -0.031804343026759746
_와 같이 붙는 밑줄은 싸이킷런에서 훈련데이터에서 유도된 속성에는 모두 _ 를 붙이기 때문에 넣은것 입니다. 사용자가 지정한 매게변수와 구분하기 위하여서 이런식으로 작성합니다.
intercept_는 실수 값 하나지만 coef_는 각 입력 특성에 하나씩 대응되는 numpy배열입니다. wave데이터셋에서는 입력 특성이 하나뿐이므로 lr.coef_도 원소를 하나만 가지고 있습니다.
훈련 세트와 테스트 세트의 성능을 확인해 보겠습니다.

다음과 같이 훈련 세트 점수와 테스트 세트 점수가 비슷함을 볼 수 있는데 이는 1차원 회귀의 경우에는 모델이 매우 단순하기 때문에 과소적합이 일어나기 때문입니다. 반면 고차원 회귀의 경우에는 과대적합이 일어날 확률이 높게 됩니다.
보스턴 주택 가격 데이터셋과 같이 복잡한 데이터셋에서 이런 현상을 살펴볼 수 있습니다.
X,y = mglearn.datasets.load_extended_boston()
X_train,X_test,y_train,y_test = train_test_split(X,y, random_state=0)
lr = LinearRegression().fit(X_train,y_train)

다음과 같이 특성이 여러개인 데이터에서는 R^2의 값이 훈련세트때는 높고 테스트 세트 때는 낮음을 볼 수 있습니다. 이는 과대적합이 일어났다는 것을 볼 수 있습니다. 이러한 문제를 해결하기 위하여 릿지 회귀가 쓰이게 됩니다.
릿지 회귀
릿지도 회귀를 위한 선형 모델이므로 최소적합법에서 사용한 것과 같은 예측 함수를 사용합니다. 하지만 릿지 회귀에서의 가중치 선택은 훈련 데이터를 잘 예측하는것 뿐 만 아닌 추가 제약 조건을 만족하기 위함도 있습니다. 릿지는 가중치의 모든 원소가 0이 되는 것이 목표입니다. 기울기를 작게 만들어서 특성의 영향력을 최소화 시키는 것입니다. 이런 제약을 규제라고 하며, 규제는 과대적합이 되지 않도록 모델을 강제로 제한한다는 의미입니다. 릿지 회귀에서 사용되는 규제는 L2 규제라고 합니다.
릿지 회귀는 linear_model.Ridge에 구현되어 있습니다.
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("훈련 세트 점수: {:.2f}".format(ridge.score(X_train,y_train)))
print("테스트 세트 점수: {:.2f}".format(ridge.score(X_test,y_test)))훈련 세트 점수: 0.89 테스트 세트 점수: 0.75
선형 회귀보다 테스트 세트에 대한 점수가 더 높습니다. 릿지는 이처럼 과대적합이 더 적어지게 됩니다. 훈련세트에서 성능은 더 나빠지지만 과대적합을 막아주어 더 일반화 된 모델이 됩니다. 관심 있는 것은 테스트 세트에 대한 성능이기 때문에 LinearRegression보다 Ridge 모델을 선택해야 합니다. Ridge는 모델을 단순하게 해주고 훈련 세트에 대한 성능 사이를 절충할 수 있는 방법을 제공합니다. 사용자는 alpha 매개변수로 훈련 세트의 성능 대비 모델을 얼마나 단순화할지를 지정할 수 있습니다. 기본값은 alpha=1.0이며, alpha값을 높이게 되면 계수가 0에 더 가깝게 만들어서 훈련 세트의 성능은 나빠지지만 일반화에는 도움을 줄 수 있습니다.
ridge10 =Ridge(alpha=10).fit(X_train,y_train)
print("훈련 세트 점수: {:.2f}".format(ridge10.score(X_train,y_train)))
print("테스트 세트 점수: {:.2f}".format(ridge10.score(X_test,y_test)))훈련 세트 점수: 0.79 테스트 세트 점수: 0.64
ridge01 = Ridge(alpha=0.1).fit(X_train,y_train)
print("훈련 세트 점수: {:.2f}".format(ridge01.score(X_train,y_train)))
print("테스트 세트 점수: {:2f}".format(ridge01.score(X_test,y_test)))훈련 세트 점수: 0.93 테스트 세트 점수: 0.772207
다음과 같이 alpha를 10으로 되게 되면 성능은 더 떨어지게 되지만 일반화가 되는데는 도움이 됩니다. alpha를 크게 해서 기울기를 0에 가깝게 만들게 되면 결국 선형회귀의 값에 수렴하게 됩니다.
여기서는 alpha가 0.1일때 성능이 좋은것을 볼 수 있는데 alpha값을 줄여서 기울기를 높이는게 정확도가 더 높은것을 볼 수 있습니다.
여기서 일단 간단히 정리를 하고 넘어가겠습니다. alpha값을 줄이면 기울기가 점점 원래대로 커지게 되면서 선형 회귀에 가깝게 되면서 모델 복잡도는 더 낮아지게 됩니다. 따라서 과소적합을 주의해야합니다. alpha값을 증가시키면 기울기가 높아지게 되면서 모델 복잡도는 더 높아지게 됩니다. 따라서 과대적합을 주의해야합니다. 따라서 alpha값을 잘 조정해서 일반화에 가까운 값을 찾아야 하는건데 여기서는 alpha값을 낮추어서 기울기를 더 높였을때 정확도가 더 높아지고 있으므로 정확도가 어디까지 높아지는 지를 찾아서 일반화에 가까운 최적점의 값을 찾으려는 것입니다.
plt.plot(ridge10.coef_,'^',label="Ridge alpha=10")
plt.plot(ridge.coef_,'s',label="Ridge alpha=1")
plt.plot(ridge01.coef_,'v',label="Ridge alpha=0.1")
plt.plot(lr.coef_,'o',label="LinearRegression")
plt.xlabel("계수 목록")
plt.ylabel("계수 크기")
plt.hlines(0,0,len(lr.coef_))
plt.ylim(-25,25)
plt.legend()

아래 그림을 통해서 coef_ 즉 계수, 기울기에 해당하는 값을 alpha값이 10, 1, 0.1일때를 각각 비교해 보았습니다.
x축은 해당 인덱스에 해당되는 계수이고 alpha값에 따라 어떻게 달라지는 것을 본것 입니다.
10으로 alpha값을 높여서 기울기를 작게 만들었을 때는 -3~3사이에 계수가 위치한 것을 볼 수 있습니다. 반면 alpha를 1로 만들어서 일때는 계수의 크기가 좀 더 높아짐을 볼 수 있습니다. 그리고 alpha가 0.1이 되면 기울기 즉 계수가 더 커짐을 볼 수 있고 선형 회귀의 경우에는 계수가 더 커져서 그림밖으로 나감을 볼 수 있습니다.
또 하나 규제를 다루는 방법으로는 alpha값을 고정하고 훈련 데이터의 크기를 변화시켜 보는 것인데 LinearRegression과 Ridge(alpha=1)을 적용한 것입니다. 이렇게 데이터셋의 크기에 따라 모델의 성능 변화를 나타낸 그래프를 학습 곡선이라고 합니다.
mglearn.plots.plot_ridge_n_samples()
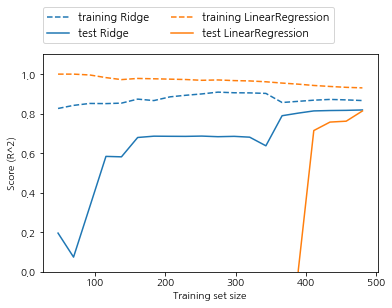
모든 데이터셋에 대해 릿지와 선형 회귀 모두 훈련 세트의 점수가 테스트 세트의 점수보다 높습니다. 릿지에는 규제가 적용되므로 릿지의 훈련 데이터 점수가 전체적으로 선형 회귀의 훈련 데이터 점수보다 낮습니다. 규제를 적용하게 되면서 훈련 데이터의 점수는 낮아지지만 과대적합을 막아주어 테스트의 정확도는 더 높습니다. 특히 더 작은 데이터 셋에서는 파란색 표가 더 유리함을 볼 수 있었습니다. 두 모델 보두 데이터가 많아질 수록 성능이 좋아지는데 데이터를 충분히 주게 되면 규제의 중요성은 낮아져서 결국 릿지회귀와 선형 회귀의 정확도는 같아지게 됩니다. 또 선형회귀의 경우 훈련데이터의 정확도가 데이터가 많아질수록 감소함을 볼 수 있는데 이는 데이터가 많아질 수록 모델이 데이터를 기억하거나 과대적합을 하기 어려워지기 때문입니다.
라쏘
선형회귀에 규제를 적용하는 릿지의 대안으로 라소가 있습니다. 릿지 회귀에서와 같이 라소도 계수를 0에 가깝게 만드려고 합니다. 하지만 방식이 조금 다르며 이를 L1규제라고 합니다. L1 규제의 결과로 라소를 사용할때 어떤 계수는 정말 0 이 됩니다. 모델에서 완전히 제외되는 특성이 생긴다는 것입니다. 따라서 특성 선택이 자동으로 이루어지게됩니다. 일부 계수를 0으로 만들게 되면 모델을 이해하기 쉬워지고 모델의 가장 중요한 특성이 무엇인지 드러나게 됩니다.
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("훈련 세트 점수: {:.2f}".format(lasso.score(X_train, y_train)))
print("테스트 세트 점수: {:.2f}".format(lasso.score(X_test,y_test)))
print("사용한 특성의 수: {:.2f}".format(np.sum(lasso.coef_ !=0)))훈련 세트 점수: 0.29 테스트 세트 점수: 0.21 사용한 특성의 수: 4.00
Lasso는 훈련세트와 테스트 결과가 모두 좋지 않을걸 보아 과소 적합이 이루어짐을 알 수 있습니다. 104개의 특성중 4개의 특성만 사용했기 때문입니다. 릿지와 마찬가지로 라소도 alpha를 이용하여 계수를 조정하게 됩니다. 과소적합을 줄이기 위해서 alpha값을 줄이면 복잡성이 증가하게 됩니다. 이때 max_iter(반복 실행하는 최대 횟수)의 기본값을 늘려야 합니다. 반복 실행 최대 횟수를 늘리지 않으면 늘리라는 경고문이 뜨게 됩니다.
lasso001=Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("훈련 세트 점수: {:.2f}".format(lasso001.score(X_train, y_train)))
print("테스트 세트 점수: {:.2f}".format(lasso001.score(X_test,y_test)))
print("사용한 특성의 수: {}".format(np.sum(lasso001.coef_!=0)))훈련 세트 점수: 0.90 테스트 세트 점수: 0.77 사용한 특성의 수: 33
이렇게 alpha값을 낮추고 max_iter값을 높여주게 되면 복잡도가 증가하여 과소 적합의 문제가 어느정도 해결됩니다.
plt.plot(lasso.coef_,'s',label="Lasso alpha=1")
plt.plot(lasso001.coef_,'^',label="Lasso alpha=0.01")
plt.plot(lasso001.coef_,'v',label="Lasso alpha=0.0001")
plt.plot(ridge01.coef_,'o',label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0,1.05))
plt.ylim(-25,25)
plt.xlabel("계수 목록")
plt.ylabel("계수 크기")
alpha=1 일때 계수 대부분이 0일 뿐만 아니라 나머지 계수들도 크기가 작다는 것을 알 수 있습니다. alpha를 0.01로 줄이면 대부분의 특성이 0이 되는 분포를 얻게 됩니다. alpha=0.0001이 되면 계수 대부분이 0이 아니고 값도 커져 꽤 규제받지 않은 모델을 얻게 됩니다. 알파를 비슷하게 했을때는 거의 비슷한 수치가 나오지만 릿지는 어떠한 계수도 0이 되지 않습니다. 보통은 릿지 회귀를 선호하지만 특성이 많고 그중 일부분만 중요하다면 라소가 더 좋은 선택일 수 있습니다. 분석하기 쉬운 모델은 라소이기 때문에 상황에 따라 선택하여 쓸 수 있습니다. 사이킷 런에서는 라소와 릿지를 결합한 ElasticNet도 제공합니다. 이렇게 결합한 엘라스틱넷은 최상의 결과를 내지만 L1규제와 L2규제를 위한 매개변수 두 개를 조정해야 합니다.
p.82
깃허브에서 소스코드/모든 시리즈 보러가기
github.com/hynki95/machine_learning
hynki95/machine_learning
Contribute to hynki95/machine_learning development by creating an account on GitHub.
github.com
IT 유튜브 타임해커 보러가기
www.youtube.com/channel/UCHsRy47P2KlE749oAAjb0Yg?view_as=subscriber
타임해커
-블록체인/인공지능 -웹개발(프론트/백) -광고(페이스북/구글/네이버) -사업계획서 작성 -비전공생을 위한 IT 공부법 채널이름은 기획,마케팅,개발을 다 같이해서 업무성과를 내는데 드는 시간을
www.youtube.com
'빅데이터&인공지능 > 인공지능' 카테고리의 다른 글
| 대표적인 그래프 탐색(BFS - UCS, DFS - IDS)과 각 탐색에 대한 평가 (0) | 2023.09.16 |
|---|---|
| 머신러닝 스터디 02-선형모델(분류 편)- 다중 클래스 분류용 선형 모델 (0) | 2020.08.10 |
| 머신러닝 스터디 02-선형회귀(회귀편)KNeighborsClassifier 분석, k-최근접 이웃 회귀 (0) | 2020.07.11 |
| 머신러닝 스터디 02- 지도학습(분류 & 회귀) (0) | 2020.07.07 |
| 머신러닝 스터디 01 - 지도학습 vs 비지도 학습, Iris data 예시 (3) | 2020.07.05 |



